One consequence of general relativity is that the curvature of space depends on the ratio of rho to rho(crit). We call this ratio Ω = rho/rho(crit). For Ω less than 1, the Universe has negatively curved or hyperbolic geometry. For Ω = 1, the Universe has Euclidean or flat geometry. For Ω greater than 1, the Universe has positively curved or spherical geometry.
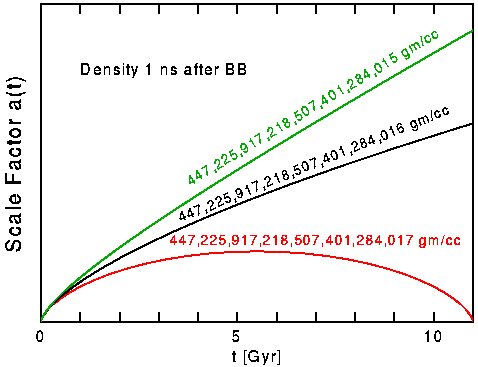
The figure above shows a(t) for three models with three different densities at a time 1 nanosecond after the Big Bang. The black curve shows the critical density case with density = 447,225,917,218,507,401,284,016 gm/cc. Adding only 1 gm/cc to this 447 sextillion gm/cc causes the Big Crunch to be right now! Taking away 1 gm/cc gives a model with Ω that is too low for our observations. Thus the density 1 ns after the Big Bang was set to an accuracy of better than 1 part in 447 sextillion. Even earlier it was set to an accuracy better than 1 part in 10E59! Since if the density is slightly high, the Universe will die in an early Big Crunch, this is called the “oldness” problem in cosmology. And since the critical density Universe has flat spatial geometry, it is also called the “flatness” problem — or the “flatness-oldness” problem. Whatever the mechanism for setting the density to equal the critical density, it works extremely well, and it would be a remarkable coincidence if Ω were close to 1 but not exactly 1.
http://www.astro.ucla.edu/~wright/cosmo_03.htm
So, 1 nanosecond after the Big Bang, the density was the universe was exactly 447,225,917,218,507,401,284,016 gm/cc. Any deviation of 1 gm/cc would cause the universe to be non-Euclidean. So, as the article states, “it is quite remarkable that Ω is anywhere close to 1 now.”
https://debatingchristianity.com/forum/viewtopic.php?p=87806#p87806
